


This is a high rank event, but very tough. R=13.5 should be visible, but the event only last 0.8 sec. The large waning gibbous moon is rising in the East, the target is high overhead.
 |
 |
 |
Kirk from Sunlit Lane, and me from Branciforte, both got recordings. Kirk at 16x and me at 8x. Clear skies. Faint, don't know how the reductions will go...
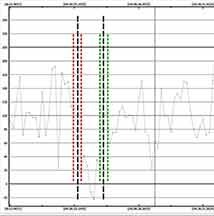
I was pleased to see that this very difficult event actually produced a solid positive. Aided by the fact I was near the centerline and also that it lasted longer than predicted. The drop occurred precisely at the predicted time of 8:36:26.0 PST, lasted 1.28s instead of 0.8s however. But the timing accuracies allow for a shorter event. I believe that the TME method was the savior. By putting a very tight mask around the target star, it minimized sky noise. Given the full moon in the sky, it was essential to reduce sky noise. It improves noise a bit by longer integration as in-camera integration reduces read-out noise. But sky noise is essential to remove by eliminating sky from your aperture as much as possible. Now, if you have a star with a small drop in brightness, this can be a trade-off as losing star-signal will be a cost. But for a full-drop occultation like this, the goal is to eliminate sky noise to the maximum extent. So, my experience now with using the TME aperture method has confirmed to me Bob Anderson's judgment and measurements that this really is a good improvement.
I recommend to my team that for faint full-drop events with any sky background at all, that they begin using the TME method. It's a slower method for the computer to slog through. The processing is ~6x real time(?) depending on your computer and memory etc I am guessing. Anyway, good for taking a short nap which I'm always in favor of.
My process for this one: Open in PyMovie. Do a "Fourier finder". Adjust the contrast range to show the star really well, (then unclick the contrast/range box so it'll stay permanent on your screen as it processes). Then put TME snap-to-center apertures on the target and two (unsaturated) reference stars; one near the target, one far from the target. The ref stars MUST stay on-chip during the entire processing of course, accounting for drift. The click on the closer ref star and turn it yellow (tracking #1) and then the farther one turn it yellow (tracking #2, to account for field rotation). The put down a 'static circular aperture' on blank sky near the target. Then let PyMovie analyze. When done, click 'plot' and look at the plots. Here, I had one bump of the Watec power cord well before the event, obvious on all light curves. The target star had a pretty clear occultation, confirmed by placing the mouse on that point and reading off the time, which corresponded accurately with the predicted time of the event, to a fraction of a second. For my images on this web page, I use "greenshot" screen capture software to grab low-res images of the light curves, and also an image of the PyMovie screen with the aperture for the target shown, and the box with the aperture parameters also shown. Then I click "save csv" and name it "RN-PyM-Bartels" for my intials, PyMovie, Asteroid name.
Then, I opened PyOTE and opened the light curve. First thing I asked for a manual/automatic block integration, which it correctly determined was 4 blocks (8x Watec setting). I accepted it. Then I clicked on the target light curve in two places; one right after the event, the other near the end of the event, and let those be my metric interval. I showed ref1 light curve as well. Since this light curve had less noise (brighter) than the other reference star I thought it better. I then started at smoothing interval 0, and increased it by 2 until the metric flatness number was minimized. It didn't matter much beyond a certain point, it stayed at the minimum. I took the first smoothing interval that arrived at that minimum. Then I zoomed in on the event and looked at the drop and decided where to place a D and an R range which must include the event. My first choice was a bit wider on the D and I did it again with a later choice on the D, but not much, just one more data point closer because that's all that seemed justified. I did want to see if it improved the depth, S/N, FP test, and perhaps gave a different D time. The answers were Yes, Yes, Yes, and "same". The timings did not change but the quality of the determination improved, and this is the one I've settled on. The duration is still 1.28s which is unusually long for a predicted 0.8 sec event, but within 2.5-sigma of the predicted interval.
(First run, choosing a D interval 1 data point left of my second choice)
magDrop report: percentDrop: 83.4 magDrop: 1.952 +/- 1.149 (0.95 ci)
DNR: 2.40
D time: [04:36:25.2670]
D: 0.6800 containment intervals: {+/- 0.0687} seconds
D: 0.9500 containment intervals: {+/- 0.2138} seconds
D: 0.9973 containment intervals: {+/- 0.5260} seconds
R time: [04:36:26.5470]
R: 0.6800 containment intervals: {+/- 0.0687} seconds
R: 0.9500 containment intervals: {+/- 0.2138} seconds
R: 0.9973 containment intervals: {+/- 0.5260} seconds
Duration (R - D): 1.2800 seconds
Duration: 0.6800 containment intervals: {+/- 0.1106} seconds
Duration: 0.9500 containment intervals: {+/- 0.2881} seconds
Duration: 0.9973 containment intervals: {+/- 0.6346} seconds
2nd PyOTE run, with D interval closer to minimum time by 1 data point. D and R times and interval turn out to be the same as 1st run.
magDrop report: percentDrop: 87.1 magDrop: 2.221 +/- 1.498 (0.95 ci)
DNR: 2.51
D time: [04:36:25.2670]
D: 0.6800 containment intervals: {+/- 0.0687} seconds
D: 0.9500 containment intervals: {+/- 0.1941} seconds
D: 0.9973 containment intervals: {+/- 0.5110} seconds
R time: [04:36:26.5470]
R: 0.6800 containment intervals: {+/- 0.0687} seconds
R: 0.9500 containment intervals: {+/- 0.1941} seconds
R: 0.9973 containment intervals: {+/- 0.5110} seconds
Duration (R - D): 1.2800 seconds
Duration: 0.6800 containment intervals: {+/- 0.1030} seconds
Duration: 0.9500 containment intervals: {+/- 0.2641} seconds
Duration: 0.9973 containment intervals: {+/- 0.5907} seconds
 |
 |
 |
 |
 |
 |
 |
 |
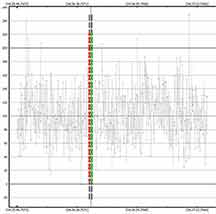 |
Looks like a miss on his data, which was done at 16x but still should have had 2 or 3 occulted points near zero if the target was roughly circular in outline. I infer that the asteroid is quite oblong and I got the long axis, and a clean miss from Kirk. Since even getting just half of one integration in the shadow would cause a 50% drop in the value, and since there is no hint of that, I believe Kirk got either a miss, or an extremely short event not visible on the data.